workshops

Statistical Distribution and Central Limit Theorem

Introduction

This workshop covers the basics of generating and visualizing statistical distributions in R using the tidyverse package. We will create three different distributions (normal, uniform, and exponential) and visualize them using kernel density plots.

Quick Overview

Importance of CLT

1: Setup and Population Generation

Loading Package: Let’s load the tidyverse package, a collection of R packages for data science, including data manipulation and visualization tools.

# Check if tidyverse is installed and install it if not
if (!requireNamespace("tidyverse", quietly = TRUE)) {
  install.packages("tidyverse")
}

# Load the tidyverse package
library(tidyverse)

Warning message:
“package ‘dplyr’ was built under R version 4.3.2”
Warning message:
“package ‘stringr’ was built under R version 4.3.2”
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.4.4     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Setting a Seed: Ensures reproducibility of results. The set.seed(123) function sets the random number generator to a fixed sequence.

# Set seed for reproducibility
set.seed(123)

Defining Population Size: Sets the number of data points for each distribution (population_size = 100,000).

# Define the population size
population_size <- 100000

Generating Populations: Creates three different distributions: normal, uniform, and exponential, each with 100,000 data points.

# Generate populations
populations <- tibble(
  normal = rnorm(population_size, mean = 50, sd = 10),
  uniform = runif(population_size, min = 0, max = 100),
  exponential = rexp(population_size, rate = 0.02)
)

Now let’s look at the first 5 rows of the tibble.

head(populations)
A tibble: 6 × 3
normaluniformexponential
<dbl><dbl><dbl>
44.3952460.4492729.292887
47.6982351.9737274.372971
65.5870896.64309 1.807305
50.7050880.3974810.901159
51.2928847.63254 1.336612
67.1506589.0385147.032041

Reshaping Data: Transforms the data into a long format, with a new column for distribution types and their values, suitable for ggplot.

# Reshape for plotting
populations_long <- populations %>%
  pivot_longer(cols = everything(), names_to = "distribution", values_to = "value")

head(populations_long)
A tibble: 6 × 2
distributionvalue
<chr><dbl>
normal 44.39524
uniform 60.44927
exponential29.29289
normal 47.69823
uniform 51.97372
exponential74.37297

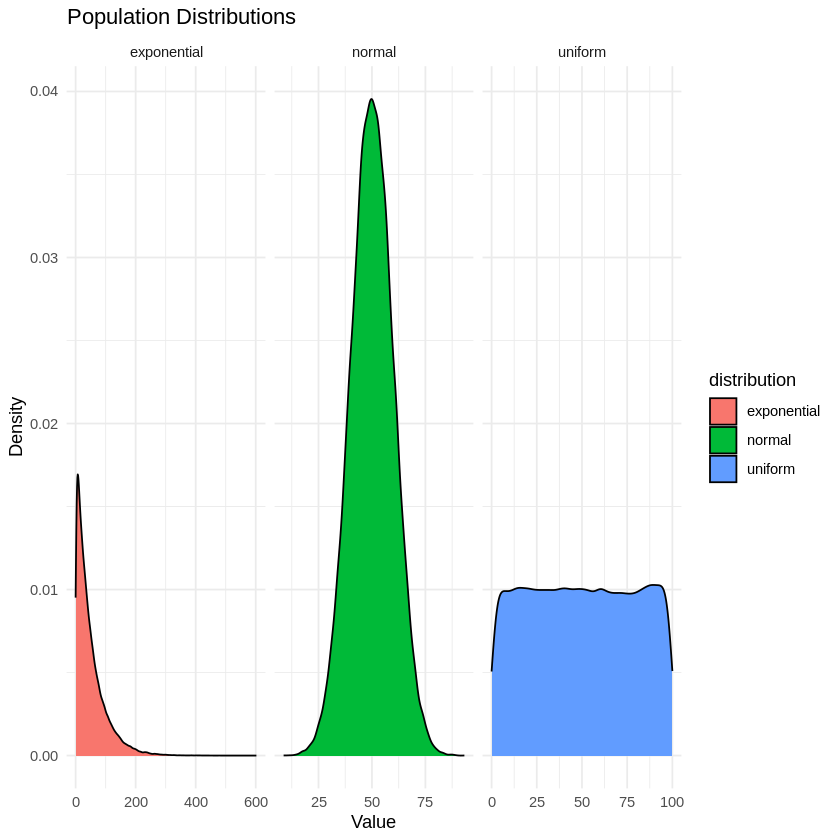
Plotting Distributions: Uses ggplot to create kernel density plots, with different facets for each distribution.

# Plot the populations using kernel density plots
ggplot(populations_long, aes(x = value, fill = distribution)) +
  geom_density() +
  facet_wrap(~ distribution, scales = "free_x") +
  labs(title = "Population Distributions", x = "Value", y = "Density") +
  theme_minimal()

png

2.Simulating Central Limit Theorem

Defining a Custom Function: sample_means is a user-defined function that takes two arguments: a population (a vector of data) and a sample_size (an integer).

# Function to take samples and compute means
sample_means <- function(population, sample_size) {
  replicate(1000, mean(sample(population, sample_size)))
}

Setting up sample sizes : This following creates a vector sample_sizes containing different sizes. These sizes represent the number of data points in each sample that will be drawn from the populations.

# Sample sizes for more intervals
sample_sizes <- c(5, 10, 20, 30, 40, 50, 100)

Replication for Robustness: Within the function, replicate(1000, …) is used to repeat a process 1000 times, enhancing the statistical robustness of the results. Sampling and Mean Calculation: In each repetition, the function randomly samples sample_size elements from population and calculates their mean. The result is an array of 1000 sample means.

# Generate sample means data
sample_means_data <- map_df(sample_sizes, function(size) {
  map_df(populations, sample_means, sample_size = size)
}) %>%
  pivot_longer(cols = everything(), names_to = "distribution", values_to = "value") %>%
  mutate(size = factor(rep(sample_sizes, each = 3000), levels = sample_sizes))

Applying Function Across Sample Sizes

Data Transformation

Creating a Dataset

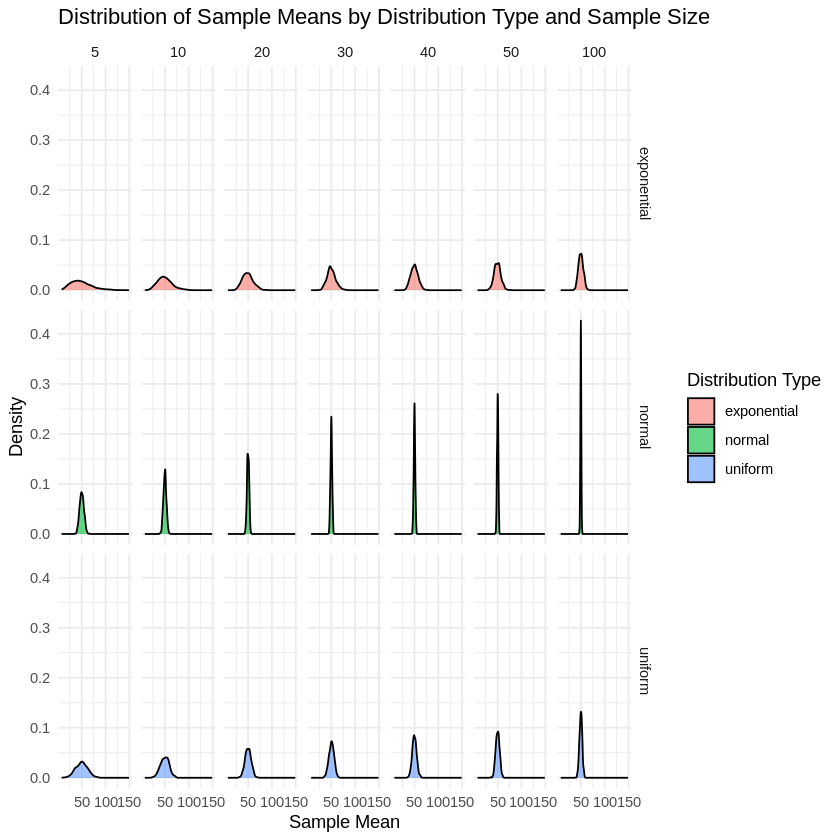
Plotting the Data:

# Plotting the distributions of sample means using kernel density plots
# Faceted by both distribution type and sample size
ggplot(sample_means_data, aes(x = value, fill = distribution)) +
  geom_density(alpha = 0.6) +
  facet_grid(distribution ~ size) +
  labs(title = "Distribution of Sample Means by Distribution Type and Sample Size",
       x = "Sample Mean",
       y = "Density") +
  theme_minimal() +
  guides(fill = guide_legend(title = "Distribution Type"))

png

References

  1. Tidyverse Package: Wickham, H. et al. (2019). Welcome to the tidyverse. Journal of Open Source Software, 4(43), 1686. https://doi.org/10.21105/joss.01686

  2. The R Project: R Core Team. The R Project for Statistical Computing. https://www.r-project.org/

  3. R Manuals: R Core Team. An Introduction to R. https://cran.r-project.org/manuals.html

  4. Understanding the Central Limit Theorem: Rice, J. A. (2007). Mathematical Statistics and Data Analysis (3rd ed.). Duxbury Press.