workshops

Error Bars and Misconceptions

Misconceptions

library(tidyverse)

set.seed(123)
ratings <- tibble(rating = rnorm(100, mean = 3, sd = 0.5))

stats <- summarise(ratings,
                   mean_rating = mean(rating),
                   sd_rating = sd(rating),
                   se_rating = sd_rating / sqrt(n()),
                   ci80 = qnorm(1 - 0.10/2) * se_rating,
                   ci95 = qnorm(1 - 0.05/2) * se_rating,
                   ci99 = qnorm(1 - 0.01/2) * se_rating)

data <- tibble(
  x = rep(1, 100),
  y = ratings$rating,
  ymin = NA_real_,
  ymax = NA_real_,
  group = "Jitter"
)

stats_data <- tibble(
  x = 2:6,
  y = rep(stats$mean_rating, 5),
  ymin = stats$mean_rating - c(stats$sd_rating, stats$se_rating, stats$ci80, stats$ci95, stats$ci99),
  ymax = stats$mean_rating + c(stats$sd_rating, stats$se_rating, stats$ci80, stats$ci95, stats$ci99),
  group = c("SD", "SE", "CI80", "CI95", "CI99")
)

data <- bind_rows(data, stats_data)


head(data)
A tibble: 6 × 5
xyyminymaxgroup
<dbl><dbl><dbl><dbl><chr>
12.719762NANAJitter
12.884911NANAJitter
13.779354NANAJitter
13.035254NANAJitter
13.064644NANAJitter
13.857532NANAJitter
 
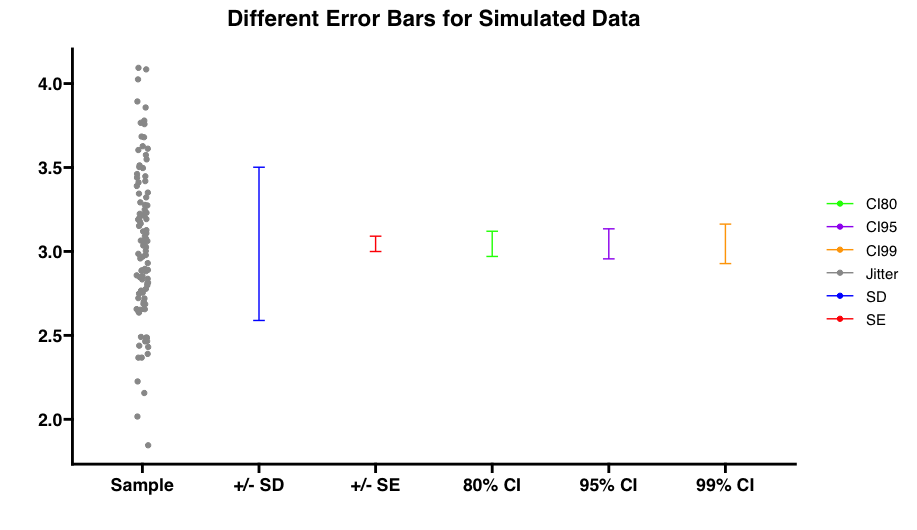
colors <- c("Jitter" = "grey60", "SD" = "blue", "SE" = "red", "CI80" = "green", "CI95" = "purple", "CI99" = "orange")

p <- ggplot(data, aes(x = as.factor(x), y = y, ymin = ymin, ymax = ymax, color = group)) +
  geom_jitter(data = filter(data, group == "Jitter"), width = 0.05) +
  geom_errorbar(data = filter(data, group != "Jitter"), width = 0.1, position = position_dodge(width = 0.8)) +
  scale_color_manual(values = colors) +
  scale_x_discrete(labels = c("Sample", "+/- SD", "+/- SE", "80% CI", "95% CI", "99% CI")) +
  labs(title = "Different Error Bars for Simulated Data", x = "Simulated Data", y = "") +
  theme(axis.title.x = element_blank(), axis.text.x = element_text(angle = 45, hjust = 1), legend.title = element_blank())

print(p)

png

library(ggplot2)


mean1 <- 5
mean2 <- 4
n <- 10
alpha <- 0.05


t_critical <- qt(1 - alpha/2, df=(n-1)*2)  

std_dev_estimated <- abs(mean1 - mean2) / t_critical * sqrt(n/2)

sem1 <- std_dev_estimated / sqrt(n)
sem2 <- std_dev_estimated / sqrt(n)
ci_half_width1 <- t_critical * sem1
ci_half_width2 <- t_critical * sem2


data <- data.frame(
  type = rep(c('STD', 'SEM', 'CI'), each = 2),
  sample = factor(rep(c('Sample 1', 'Sample 2'), 3)),
  mean = c(mean1, mean2, mean1, mean2, mean1, mean2),
  ymin = c(mean1 - std_dev_estimated, mean2 - std_dev_estimated,
           mean1 - sem1, mean2 - sem2,
           mean1 - ci_half_width1, mean2 - ci_half_width2),
  ymax = c(mean1 + std_dev_estimated, mean2 + std_dev_estimated,
           mean1 + sem1, mean2 + sem2,
           mean1 + ci_half_width1, mean2 + ci_half_width2)
)


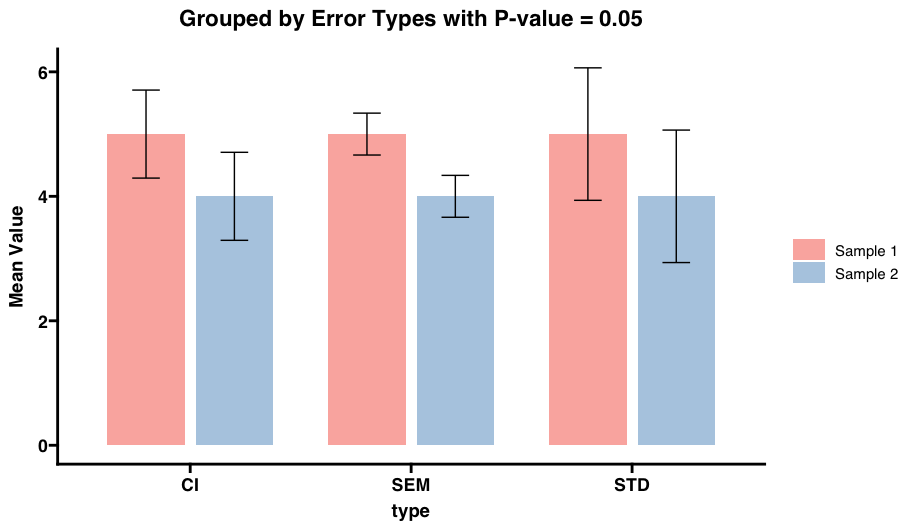
p <- ggplot(data, aes(x = type, y = mean, fill = sample)) +
  geom_bar(stat = "identity", position = position_dodge(width = 0.8), width = 0.7) +
  geom_errorbar(aes(ymin = ymin, ymax = ymax), position = position_dodge(width = 0.8), width = 0.25) +
  theme_minimal() +
  labs(title = "Grouped by Error Types with P-value = 0.05", y = "Mean Value") +
  scale_fill_brewer(palette = "Pastel1", name = "Sample")


print(p)

png

Guidance on Using Standard Deviation, Standard Error, and Confidence Intervals as Errors When Plotting Data

  1. Standard Deviation (SD):
    • Use SD to represent the variability or dispersion of a set of data points around the mean.
    • SD is most appropriate when you want to show how much individual measurements in a dataset vary from the average value.
    • Ideal for datasets where you’re interested in the distribution of values itself, rather than estimating the reliability of a sample mean.
  2. Standard Error (SE):
    • Use SE to represent the precision of the sample mean as an estimate of the population mean.
    • SE is calculated as the standard deviation of the sample divided by the square root of the sample size.
    • Appropriate for datasets where the goal is to infer about the population from a sample, especially in cases where multiple samples are compared.
  3. Confidence Intervals (CI):
    • Use CIs to provide a range within which the true population parameter is expected to lie, with a certain level of confidence (usually 95% or 99%).
    • CI gives an estimated range of values which is likely to include the population parameter, based on the sample data.
    • Ideal for both visualizing the precision of sample estimates and making inferences about the population, particularly useful in comparative studies.

Important Points:

Considerations:

Reference